The purpose of this page is to provide basic guidance on high-level spatial data concepts and what to consider when recording spatial data in a New Zealand context. In particular, recommended spatial data types, the use of New Zealand’s current coordinate systems, and current metadata standards. New Zealand is almost unique in the world where we have to account for the anti-meridian line, which many Geographic Information Systems (GIS) struggle with, so some guidance is also included for handling this. Please note this page only covers vector data (which uses point and lines segments to represent locations) and not raster data, which uses cells to represent locations.
Spatial concepts
Spatial data is commonly described in terms of layers, features and geometry. In the context of a relational database, a layer equates to a table in the database, a feature to a record in the table, and the geometry to a field in the record with a spatial data type. In a similar way that a field can be defined as having a data type of integer or text (for example), spatial databases allow the field to have a geometry (or geography) data type. As integers or strings data types support particular operations (e.g. addition or concatenation), spatial data types have their own suite of operations (e.g. buffer and intersection to name only two of many).
Spatial data features are defined in particular geometry types such as point, line or polygon. Some systems allow different geometry types to be mixed in one layer (or table), but many do not; so this is an important consideration when designing a system. A complete list of the different geometry types is listed in Table 1 below.
Spatial databases or file types are designed to work seamlessly with GISs and hide any complexity of the implementation from the user. So although some detail about spatial data types is covered below, it is not necessary to understand the detail of how it's implemented to be able to use a GIS.
Spatial data types
OGC Simple Feature access - The Well-Known Text and Well-Known Binary formats
Simple Feature access is a fundamental storage format for spatial data. It's widely implemented in RDMS systems including:
- My SQL
- PostgreSQL/PostGIS
- SQLite/Spatial Lite
- Oracle Spatial
- IBM DB2
- Informix
- Microsoft SQL Server (since version 2008).
- OGC GeoPackage
Find a full list of implementations of the Open Geospatial Consortium's (OGC) Simple Feature access format on the OGC website.
Open Geospatial Consortium's (OGC) website
The OGC standard 19125-1 (part 1) defines the architecture, and OGC standard 19125-2 (part 2) defines the SQL implementation. The specification is on the OGC website.
Table 1 below lists the geometry types with examples in Well-Known Text (WKT) format. WKT is recommended where interoperability is the priority.
Table 1: Well-Known Text (WKT) representation of geometries
| Geometry Type | WKT Literal Representation | Comment |
|---|---|---|
| Point | Point (10 10) | a Point. |
| LineString | LineString ( 10 10, 20 20, 30 40) | a LineString with 3 points. |
| Polygon | Polygon ((10 10, 10 20, 20 20, 20 15, 10 10)) | a Polygon with 1 exteriorRing and 0 interiorRings. |
| Multipoint | MultiPoint ((10 10), (20 20)) | a MultiPoint with 2 points. |
| MultiLineString | MultiLineString ( (10 10, 20 20), (15 15, 30 15) ) | a MultiLineString with 2 linestrings. |
| MultiPolygon | MultiPolygon ( ((10 10, 10 20, 20 20, 20 15, 10 10)), ((60 60, 70 70, 80 60, 60 60 )) ) | a MultiPolygon with 2 polygons. |
| Point | Point Z (10 10 5) | a 3D Point. |
| Point | Point ZM (10 10 5 40) | the same 3D Point with an M "modifier" value of 40. M values are system or user-defined. |
| Point | Point M (10 10 40) | a 2D Point with M value of 40. |
| GeomCollection | GeometryCollection ( POINT (10 10), POINT (30 30), LINESTRING (15 15, 20 20) ) | A GeometryCollection consisting of 2 Point values and a LineString value. |
| Polyhedron | Polyhedron Z ( ((0 0 0, 0 0 1, 0 1 1, 0 1 0, 0 0 0)), ((0 0 0, 0 1 0, 1 1 0, 1 0 0, 0 0 0)), ((0 0 0, 1 0 0, 1 0 1, 0 0 1, 0 0 0)), ((1 1 0, 1 1 1, 1 0 1, 1 0 0, 1 1 0)), ((0 1 0, 0 1 1, 1 1 1, 1 1 0, 0 1 0)), ((0 0 1, 1 0 1, 1 1 1, 0 1 1. 0 0 1)) ) | A polyhedron cube, corner at the origin and opposite corner at (1, 1, 1). |
| Tin (Triangular irregular networks) | Tin Z ( ((0 0 0, 0 0 1, 0 1 0, 0 0 0)), ((0 0 0, 0 1 0, 1 0 0, 0 0 0)), ((0 0 0, 1 0 0, 0 0 1, 0 0 0)), ((1 0 0, 0 1 0, 0 0 1, 1 0 0)), ) | A digital representation of a surface. This example is of a tetrahedron (4 |
Well-Known Binary (WKB) representation for geometry
WKB is the binary form of the above WKT representation of geometries. It is recommended for systems that require more efficient data transmission than the WKT format and is implemented as ST_Geometry subclasses: ST_Point, ST_LineString, ST_Polygon, ST_MultiPoint, ST_MultiLineString, ST_MultiPolygon. As it is not human readable there is no value in including an example here.
Extended Well-Known Text (EWKT) Representation for Geometry
EWKT is not an official standard, but a variation on the WKT format where the spatial reference system identifier (SRID) is included. The SRID is defined using the EPSG code**.
It's worth noting as it's commonly used by PostGIS and Oracle spatial databases.
The following is an example of how a record with a geometry in EWKT format can be inserted in a PostGIS database:
INSERT INTO example_table(id, geom)
VALUES (1, 'SRID=4326;MULTIPOLYGON(((175 -40,185 -40, 185 -45, 175 -45,175 -40)))');
Point coordinate representation
There may be cases where there is no option to store point coordinates in a database that supports spatial data types or the coordinates are only intended to be read by people. Storing coordinates in anything other than a spatial database reduces or removes the ability to use the data in a GIS and run queries optimised with spatial indexes, so this is not an ideal option. However, if it is to be done than coordinates should be stored as floating point values, unless human-readability is the priority, in which case recording coordinates in degrees, minutes and seconds is the most meaningful. Points can be represented as two columns as an x/y coordinate pair. Column names that are most commonly used in this case are longitude/latitude, lon/lat, long/lat, x/y, northing/easting depending on the coordinate system type.
ISO 6709: Standard representation of geographic point location by co-ordinates provides further guidance for these coordinate notations.
The following are examples of different coordinate notation types:
- Decimal degrees -41.27843, 174.77663,
- Degrees, minutes, seconds: 41°16’42.32268” S, 174°46’35.85129” E
- Grid coordinates formatted (NZTM2000): 5428811 mN, 1748789 mE
- Grid coordinates decimal (NZTM2000): 5428811.0, 1748789.0
Coordinate axis order
Axis order is the order that coordinates pairs are stored in; either Y/X or X/Y where X is the easting or longitude and Y is northing or latitude. Different spatial reference systems and software systems use different axis orders as there's no universal standard. Land Information New Zealand (LINZ) recommends following:
- For simple usage use X/Y order. This is preferable to maximise compatibility.
- When using WKT geometry representations use longitude/latitude or easting/northing axis order. All current known WKT implementations in database systems follow this order.
- Use the axis order specification as defined by the European Petroleum Survey Group (EPSG) coordinates system parameter database (see examples below). This will be required when using interoperable API services from OGC.
Coordinate systems
Coordinate types
There are 4 main types of coordinate system:
Geographic (or geodetic) systems
These relate the physical location of a point on a curved surface with a coordinate in terms of latitude, longitude, and ellipsoidal height. In New Zealand, the New Zealand Geodetic Datum 2000 (NZGD2000) is the official datum. For accuracies of a metre or worse, it is practically the same as using the World Geodetic System 1984 (WGS84) which, as the name suggests, is a global geographic system.
Geographic coordinate system
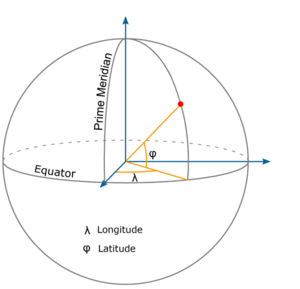
Cartesian systems
These systems have coordinates that measure the position of a point from a defined origin along perpendicular axes. Projected systems are a subset of cartesian system, but generally, the term cartesian is usually used for small localised maps or technical drawings.
Cartesian coordinate system
Projected (or geometric) systems
Projected systems are a subset of cartesian system that maps the earth on a flat surface. It is not possible to represent geographic coordinates on a flat surface without introducing some sort of distortion. This can be visualised using the peel of an orange: it is not possible to lay the entire peel flat without breaking it in some way.
A projection is used to manage these distortions in a predictable way. Projections are chosen to maintain certain characteristics (to minimise the impact of the distortion). Different projections can preserve direction, shape, area, distance and shortest route, however no projection can preserve all of these.
An additional benefit of projections is that they have units of metres, which lets users measure meaningful distances directly from a map.
Many different types of projection can be used, but the most common are related to different geometric shapes such as cylinders, cones and planes. In New Zealand, most maps are produced using the Transverse Mercator projection, which is based on a cylinder that lies on its side so that it is coincident with a line of longitude (called the central meridian).
The official projection for New Zealand topographic mapping is called the New Zealand Transverse Mercator 2000 or NZTM2000 for short.
The de facto coordinate system for web mapping applications is Web Mercator, a projected system which is used worldwide.
Vertical coordinate systems
Vertical coordinate systems record heights measured above (or below) a reference surface (datum).
In New Zealand, there are 3 main vertical datums that are commonly used: the New Zealand Vertical Datum 2016 (NZVD2016), local mean sea level datums and NZGD2000 ellipsoidal heights.
Linear referencing
Linear referencing records the position of features along a known linear feature. Either points or ranges can be recorded this way. The position of highway assets along a highway network is an example where linear referencing can be used.
Linear Reference System
Geographic vs projected (geometric) coordinate types when storing data
Of the 4 coordinate types listed above, geographic and geometric are the most widely used. Often it isn't clear which of these 2 coordinate types is best to use for a particular dataset. Each has its own advantages and disadvantages.
Advantages and disadvantages of geographic vs geometric coordinate types
| Geography | Geometric |
|---|---|
| Stores data in longitude/latitude coordinates | Stores data in projected coordinates |
| Databases have fewer spatial functions | Databases have more spatial functions |
| Database functions will be relatively slower | Database functions will be relatively faster |
| No need to consider projection or accuracy limits across large regions | Need to consider projection or accuracy limits across large regions |
| Will need conversion to a projected coordinate system for visualisation | Likely won't need conversion to a projected coordinate system for visualisation |
| Not best suited to 3D modelling | Suited for 3D modelling |
| Good if data is primarily being stored | Good if data is primarily being used for visualisation |
Selecting the correct coordinate system for NZ applications
Geographic coordinate reference systems
- New Zealand Geodetic Datum 2000 (NZGD2000), EPSG: 4167*.
Use when:- Data extents are greater than mainland New Zealand.
- Sub-metre accuracy is important.
- Data is primarily being stored rather than being used for creating maps.
- World Geodetic System 1984 (WGS84), EPSG: 4326.
Use when:- Data will be used with other global datasets.
- Sub-metre accuracy isn't important.
- Some spatial databases only support WGS84 as a coordinate reference system.
Geometric coordinate reference systems
- New Zealand Transverse Mercator 2000 (NZTM2000), EPSG: 2193.
Use when:- Creating 2D maps of features in mainland New Zealand.
- Metric units are needed.
- Creating web tile services covering the New Zealand mainland.
- Also, see the New Zealand offshore islands and Ross Sea Region projections for mapping in these localised areas.
- New Zealand Continental Shelf Lambert Conformal 2000
Use when:- As for NZTM2000 but when a large longitudinal coverage extending beyond mainland New Zealand is needed
- WGS 84 / Pseudo Web Mercator, EPSG: 3857.
Use when:- Displaying data on web maps in a global context.
- Creating web tile services is easier for web developers.
- Metric units are needed.
The obsolete New Zealand Geodetic Datum 1949 and New Zealand Map Grid 1949 should not be used as these have long since been replaced by NZGD 2000 and NZTM 2000 respectively.
More guidance on datums, projections and heights
Coordinate transformations
Data stored in one coordinate system can easily be transformed into other coordinate systems. Most spatial databases and desktop apps do this simply and quickly and on the fly, meaning a transformed copy of the data doesn't need to be saved as a duplicate.
Most desktop GISs have a user-friendly interface for transforming coordinates, and spatial APIs or database functions are also simple. For example in a PostGIS database the function:
ST_Transform(shape, 2193)
converts geometries in the "shape" column to the NZTM 2000 projection which is referenced by EPSG number "2193".
Anti-Meridian
New Zealand is almost unique in the world where we have to manage data that crosses the anti-meridian (the line of longitude at 180 degrees). Geographic information systems generally aren't designed very well to seamlessly handle data that crosses the anti-meridian and one of the following workarounds will need to be applied to get the data to function and display correctly in the GIS.
- Split features that cross the anti-meridian.
e.g.: MULTIPOLYGON(((175 -40,180 -40, 180 -45, 175 -45,175 -40)),((-180 -40,-185 -40, -185 -45, -180 -45,-180 -40)))
- Transform the data so longitude coordinates are recorded in terms of 0 to 360 degrees rather and +/-180 degrees.
e.g.: MULTIPOLYGON(((175 -40,185 -40, 185 -45, 175 -45,175 -40)))
*EPSG Codes
EPSG codes provide a unique numeric identifier for recognised coordinate systems. They are very convenient and already referenced in this page above. Codes can be found on https://spatialreference.org/
Although not an official standard, it is an industry-standard and widely used in geospatial software. For example databases such as PostGIS and Oracle support the EWKT format, which includes the EPSG code with the WKT geometry.
Precision, accuracy and scale
For spatial features, accuracy describes how close the geometry of the feature is to its location in the real world. Precision describes how consistent geometries of the same feature are relative to each other.
Documenting how geometries were captured (ideally in a layer's metadata) is very important so users of the dataset can understand the accuracy and therefore limitations of the data. It is also recommended that coordinates are stored with a numerical precision appropriate for the scale they were recorded at and intended to be used at. For example, it would be misleading to record the location of a feature with great precision if it was roughly calculated using a small scale map. The following table shows approximate linear resolutions for fractions of a degree.
Table 2: Resolution for fractions of a degree with usage examples
| Decimal degrees | Approximate linear resolution | Example of feature being located |
|---|---|---|
| 1 | 100 km | Region |
| 0.01 | 1 km | City |
| 0.001 | 100 m | Neighbourhood |
| 0.0001 | 10 m | House |
| 0.00001 | 1 m | Entranceway to house |
| 0.000001 | 10 cm | Doormat in entranceway |
| 0.0000001 | 1 cm | Mouse sitting on doormat |
If you have suggestions for how this page can be improved, please email geostandards@linz.govt.nz