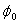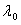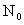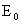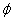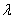Projections are used to convert points on a 3-dimensional curved surface of the Earth onto a 2-dimensional flat surface. Unlike geodetic datums, which are used to maintain coordinate accuracy, projections deliberately distort the data for representing a section of the Earth as a map, plan and on-screen visualisation.
New Zealand Map Grid (NZMG) was the national projection of New Zealand until it was replaced by the New Zealand Transverse Mercator projection. Coordinates in either of these projections are usually displayed in terms of Northing and Easting (N,E), while geodetic datum coordinates are displayed in terms of Latitude and Longitude (ϕ, λ).
New Zealand Transverse Mercator 2000
Coordinate systems used in New Zealand
For most users, NZMG transformations can be completed using common spatial software or by using our online coordinate converter.
Converting from NZMG to NZTM2000
A three-step process is used to convert coordinates from New Zealand Map Grid (NZMG) to New Zealand Transverse Mercator 2000 (NZTM2000).
- De-project NZMG coordinates to NZGD1949 (described below)
- Convert NZGD1949 geographic coordinates to NZGD2000
- Project NZGD2000 geographic coordinates onto NZTM2000
This process is used by our online coordinate converter and downloadable software.
Geodetic software and downloads
Transforming coordinates between NZMG and NZGD1949
Projection parameters
The equations on this page use the following definitions of the parameters, which are common to all projection transformations used in New Zealand.
| Symbol | Parameter |
|---|---|
| a | Semi-major axis of reference ellipsoid |
| f | Ellipsoidal flattening |
| Origin latitude | |
| Origin longitude | |
| False Northing | |
| False Easting | |
| Latitude of computation point | |
| Longitude of computation point | |
| N | Northing of computation point |
| E | Easting of computation point |
Transformations from NZGD1949 to NZMG
Note that these conversions require the latitude and longitude to be expressed in decimal degrees, where north and east are positive.
i) Calculate ΔΨ and Δλ:
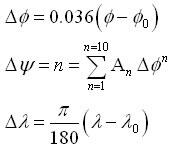
ii) Calculate a complex polynomial function of the complex number θ = ΔΨ + iΔλ:
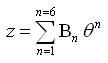
iii) Calculate the northing N and easting E from x and y by expressing the complex number z in terms of its real and imaginary parts z = x + iy:
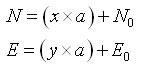
Transformations from NZMG to NZGD1949
The conversion from NZMG to NZGD1949 geographic coordinates (θ, λ) involves an iterative approximation (which is used to reverse step ii) above).
i) Derive the complex number z:
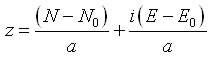
ii) Determine the complex number θ as a series of approximations (θ0 , θ1 , θ2 and so on). Two iterations of this formula will give millimetre transformation accuracy. The first approximation is:
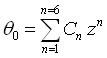
iii) Successive approximations are obtained by applying the formula:
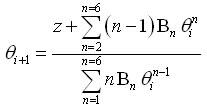
iv) Calculate the latitude and longitude, by expressing θ in terms of its real and imaginary parts θ = ΔΨ + iΔλ:
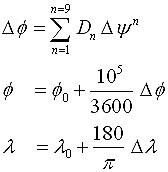
NZMG coefficients
| Coefficient | Real Part | Imaginary Part |
|---|---|---|
| A1 | 0.6399175073 | |
| A2 | -0.1358797613 | |
| A3 | 0.063294409 | |
| A4 | -0.02526853 | |
| A5 | 0.0117879 | |
| A6 | -0.0055161 | |
| A7 | 0.0026906 | |
| A8 | -0.001333 | |
| A9 | 0.00067 | |
| A10 | -0.00034 | |
| B1 | 0.7557853228 | 0 |
| B2 | 0.249204646 | 0.003371507 |
| B3 | -0.001541739 | 0.041058560 |
| B4 | -0.10162907 | 0.01727609 |
| B5 | -0.26623489 | -0.36249218 |
| B6 | -0.6870983 | -1.1651967 |
| C1 | 1.3231270439 | 0 |
| C2 | -0.577245789 | -0.007809598 |
| C3 | 0.508307513 | -0.112208952 |
| C4 | -0.15094762 | 0.18200602 |
| C5 | 1.01418179 | 1.64497696 |
| C6 | 1.9660549 | 2.5127645 |
| D1 | 1.5627014243 | |
| D2 | 0.5185406398 | |
| D3 | -0.03333098 | |
| D4 | -0.1052906 | |
| D5 | -0.0368594 | |
| D6 | 0.007317 | |
| D7 | 0.01220 | |
| D8 | 0.00394 | |
| D9 | -0.0013 |