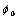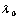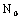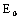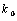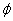Projections are used to convert points on a 3-dimensional curved surface of the Earth onto a 2-dimensional flat surface. Unlike geodetic datums, which are used to maintain coordinate accuracy, projections deliberately distort the data for representing a section of the Earth as a map, plan and on-screen visualisation.
Transverse Mercator projection coordinates are usually given in terms of Northing and Easting (N,E) while geodetic datum coordinates are in terms of Latitude and Longitude (ϕ, λ).
For most users, transverse Mercator transformations can be completed using common spatial software or by using our online coordinate converter.
The mathematical formulae which are used to calculate a transverse Mercator projection coordinate transformation are defined in the Standard for New Zealand Geodetic Datum 2000 Projections.
Standard for New Zealand Geodetic Datum 2000 Projections: Version 2
Projection parameters
The equations on this page use the following definitions of the parameters, which are common to all projection transformations used in New Zealand.
| Symbol | Paramater |
|---|---|
| a | Semi-major axis of reference ellipsoid |
| f | Ellipsoidal flattening |
| Origin latitude | |
| Origin longitude | |
| False Northing | |
| False Easting | |
| Central meridian scale factor | |
| Latitude of computation point | |
| λ | Longitude of computation point |
| N | Northing of computation point |
| E | Easting of computation point |
Projection constants
Before a transverse Mercator projection transformation can be completed, several additional parameters need to be computed: the constants b, e2 and m0.
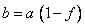
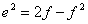

m0 is obtained by evaluating m using ϕ0
Converting geographic to transverse Mercator coordinates
First determine (m, ρ, υ) at the computation point (ϕ, λ):
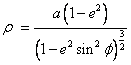
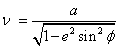
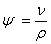
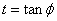
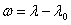
The projection northing (N) of the computation point is then determined:

The projection easting (E) of the computation point is determined last:

Converting transverse Mercator projection to geographic coordinates
First determine N1, m1, n, G, σ and ϕ1:
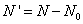
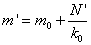
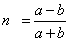
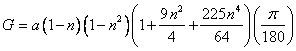
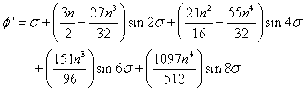
Then determine ρ1, υ1, Ψ1, t1, E1 and x:
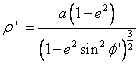
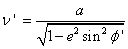
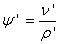
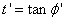
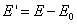

The latitude of the computation point is then computed:

Finally the longitude of the computation point is determined:
Grid convergence and point scale factor
Grid convergence (γ) is the angle at a point between true north and grid (projection) north. The point scale factor (κ) is the scale factor at a point that changes with increasing distance from the central meridian.
Both γ and κ can be evaluated for the coordinates in the transverse Mercator and Lambert conformal projections using the respective formulas defined in Standard for New Zealand Geodetic Datum 2000 Projections.
Standard for New Zealand Geodetic Datum 2000 Projections: Version 2 - LINZS25002