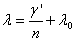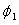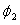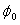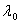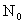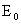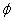Projections are used to convert points on a 3-dimensional curved surface of the Earth onto a 2-dimensional flat surface. Unlike geodetic datums, which are used to maintain coordinate accuracy, projections deliberately distort the data for representing a section of the Earth as a map, plan and on-screen visualisation.
One of the more commonly used examples of a Lambert conformal conic projection in New Zealand is the New Zealand Continental Shelf Lambert conformal 2000 (NZCS2000).
New Zealand Continental Shelf Lambert conformal 2000 (NZCS2000)
Lambert conformal conic projection coordinates are usually displayed in terms of northing and easting (N,E) and while geodetic datum coordinates are displayed in terms of latitude and longitude (ϕ, λ).
Coordinate systems used in New Zealand
For most users, Lambert conformal conic transformations can be completed using common spatial software or by using our online coordinate converter.
Projection parameters
The equations on this page use the following definitions of the parameters, which are common to all projection transformations used in New Zealand.
| Symbol | Parameter |
|---|---|
| a | Semi-major axis of reference ellipsoid |
| f | Ellipsoidal flattening |
| Latitude of first standard parallel | |
| Latitude of second standard parallel | |
| Origin latitude | |
| Origin longitude | |
| False Northing | |
| False Easting | |
| Latitude of computation point | |
| λ | Longitude of computation point |
| N | Northing of computation point |
| E | Easting of computation point |
Projection constants
The constants e, n, F, and ρ0 must be calculated before a Lambert conformal projection transformation can be completed.
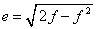
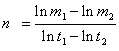
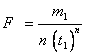
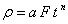
where:
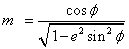
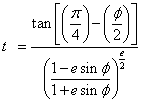
m1 and m2 are obtained by evaluating m using ϕ1 and ϕ2
t0, t1 and t2 are obtained by evaluating t using ϕ0, ϕ1, and ϕ2
ρ0, is obtained by evaluating ρ using t0
Transforming geographic coordinates to Lambert conformal projection coordinates
Determine t and ρ at the using the latitude of the computation point (ϕ) and the formulae above, then evaluate θ at the longitude of the computation point (λ):
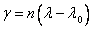
The projection northing ( N ) of the computation point is computed next:
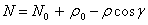
Then the projection easting ( E ) of the computation point is computed:
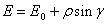
Transforming Lambert conformal projection coordinates to geographic coordinates
Determine N1, E1, ρ1, t1 and θ1:
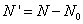
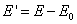
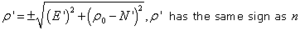
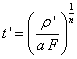

The latitude of the computation point needs to be computed iteratively. The first approximation is obtained using:
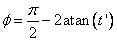
This initial estimate of ϕ is then substituted into:
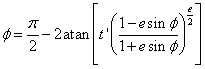
This value of ϕ should be re-substituted into the above formula until successive values do not change.
The longitude of the computation point (λ) is determined using: