The accuracy of a coordinate or height can be measured in different ways. To ensure that information about coordinates is provided in a way that is helpful to a range of users, Toitū Te Whenua describes network accuracy by using tiers, local accuracy by class, and combined accuracy by order.
The tier, class and order classification system was introduced on 24 May 2010. It is used in Landonline and the Geodetic Database.
Tiers describe network accuracy
Tiers are used to describe network accuracy, representing the uncertainty of a coordinate in relation to a datum. It represents the standalone accuracy of a coordinate, with circular error for coordinates and linear error for heights.
The equation to compute the maximum horizontal error (HE) and maximum vertical error (VE) for a coordinate is shown below. σ is the standard deviation of the coordinate component. Errors are calculated at the 95% confidence level.
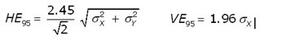
Tiers are defined in the Standard for tiers, classes, and orders of LINZ data (LINZS25006). They are summarised in the table below.
Standard for tiers, classes, and orders of LINZ data LINZS25006
| Tier | Accuracy (m) |
|---|---|
| A | 0.05 |
| B | 0.10 |
| C | 0.15 |
| D | 0.20 |
| E | 0.25 |
| F | 0.35 |
| G | 0.50 |
| H | 1 |
| J | 2 |
| K | 5 |
| M | 10 |
| N | 20 |
| P | 50 |
| R | 100 |
Classes describe local accuracy
Classes are used to describe local accuracy, representing the accuracy of a coordinate relative to other nearby coordinates. This is often described as observation accuracy, which is used by surveyors assessing the accuracy of a measurement between two geodetic marks.
Classes have 2 components: a constant term (c) and a distance-dependent term (p). To meet the class accuracy criteria, a coordinate must be tested against all coordinates of the same or higher class within a specified distance, even when there is no direct observation between them.
The equation to compute the maximum error between 2 coordinates is shown below. D is the distance between the coordinates. Error is calculated at the 95% confidence level.
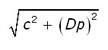
Note that the distance used in this equation depends on the type of coordinate that is being assessed:
- Horizontal coordinate accuracy is assessed with the horizontal distance.
- Vertical (height) accuracy of control marks and non-boundary survey marks is assessed with the slope distance.
- Vertical (height) accuracy of boundary marks is assessed with the vertical distance.
Classes are defined in the Standard for tiers, classes, and orders of LINZ data (LINZS25006). They are summarised in the table below.
Standard for tiers, classes, and orders of LINZ data LINZS25006
| Class | Constant term (c) (m) | Distance dependent term (p) (m) |
|---|---|---|
| I | 0.003 | 1 x 10-8 |
| II | 0.003 | 3 x 10-8 |
| III | 0.003 | 1 x 10-7 |
| IV | 0.003 | 3 x 10-7 |
| V | 0.003 | 1 x 10-6 |
| VI | 0.01 | 3 x 10-6 |
| VII | 0.01 | 1 x 10-5 |
| VIII | 0.01 | 5 x 10-5 |
| IX | 0.02 | 1 x 10-4 |
| X | 0.03 | 1.5 x 10-4 |
| XI | 0.06 | 1.5 x 10-4 |
| XII | 0.30 | 6 x 10-4 |
| XIII | 0.60 | 1 x 10-3 |
| XIV | 1 | 3 x 10-3 |
| XV | 3 | 1 x 10-2 |
| XVI | 10 | 3 x 10-2 |
Orders describe combined accuracy
Orders combine the tier and class accuracy requirements into a single category, which enables the accuracy of all coordinates to be described in a consistent way. A coordinate must pass both the network and local accuracy tests to be assigned an order.
There are 2 different order classifications: one is used for geometric coordinates (latitude, longitude, ellipsoidal height), such as New Zealand Geodetic Datum 2000 (NZGD2000), and the other is used for normal-orthometric heights, such as New Zealand Vertical Datum 2016 (NZVD16).
Orders are defined in the Standard for tiers, classes, and orders of LINZ data (LINZS25006). They are summarised in the table below.
Standard for tiers, classes, and orders of LINZ data LINZS25006
| Landonline Order | Horizontal Tier | Horizontal Class | Vertical Tier | Vertical Class |
|---|---|---|---|---|
| 0 | A | II | A | II |
| 1 | A | III | B | IV |
| 2 | B | V | E | VI |
| 3 | B | VI | F | VII |
| 4 | C | VII | F | VIII |
| 5 | C | VIII | F | IX |
| 6 | C | X | - | - |
| 7 | D | XI | - | - |
| 8 | G | XII | - | - |
| 9 | K | XIV | - | - |
| 10 | N | XV | - | - |
| 11 | P | XVI | - | - |
| 12a | - | - | - | - |
| 1V | - | - | E | VI |
| 2V | - | - | F | VII |
| 3V | - | - | F | IX |
| 4V | - | - | G | X |
| 5V | - | - | H | XII |
| 6Vb | - | - | - | - |
| a Order 12 includes all coordinates that do not achieve the Order 11 requirements b Order 6V includes all coordinates that do not achieve the Order 5V requirements |